Capítulo 12 Diversidade Taxonômica

Pré-requisitos do capítulo

Pacotes e dados que serão utilizados neste capítulo.

## Pacotes
library(devtools)
library(ecodados)
library(vegan)
library(ggplot2)
library(BiodiversityR)
library(hillR)
library(betapart)

## Dados
composicao_especies <- ecodados::composicao_anuros_div_taxonomica
precipitacao        <- ecodados::precipitacao_div_taxonomica

12.1 Aspectos teóricos

A diversidade biológica é um conceito multifacetado que pode ser definido e analisado de diferentes maneiras (e.g. diversidade genética, taxonômica, funcional, filogenética, ecossistêmica, etc.) (Magurran and McGill 2011; Gotelli and Chao 2013). Whittaker (1960, 1972) particionou a diversidade em três componentes: i) diversidade alfa que é caracterizada pela diversidade dentro do habitat ou unidade amostral, ii) diversidade beta que é caracterizada pela variação na diversidade entre habitats ou unidades amostrais, e iii) diversidade gama que é caracterizada pela combinação da diversidade alfa e beta ou definida como a diversidade regional englobando todos os habitat ou unidades amostrais. Portanto, não existe um método que quantifique todos os parâmetros associados à diversidade biológica. Consequentemente, a escolha da métrica de diversidade dependerá: i) do objetivo do estudo, e ii) das informações disponíveis para o pesquisador.

Neste capítulo, iremos abordar a diversidade taxonômica que ignora a relação de parentesco entre as espécies (e.g. diversidade filogenética - Capítulo 13) e as diferentes funções que as espécies realizam no ecossistema (e.g. diversidade funcional - Capítulo 14). Na diversidade taxonômica, pesquisadores estão interessados na riqueza de espécies (e.g. número de espécies), na distribuição de abundância das espécies (e.g. fato que algumas espécies são comuns e outras raras) e/ou diversidade de espécies (e.g. índices que descrevem a relação entre a riqueza e a distribuição da abundância relativa das espécies) nas localidades.

12.2 Diversidade alfa

12.2.1 Riqueza de espécies ou número de espécies

Riqueza de espécies é uma métrica intuitiva e de fácil compreensão, uma vez que se refere ao número de espécies observadas em uma localidade. É importante ter em mente que a riqueza de espécies é influenciada pelo esforço amostral e sua estimativa real é um imenso desafio (Magurran and McGill 2011). Comparações entre comunidades com diferenças no número de amostragens ou abundância das espécies devem ser realizadas por meio de rarefações (veja Capítulo 10), enquanto que o número de espécies não detectadas pode ser estimado pelos estimadores de riqueza (veja Capítulo 11). Embora raramente usados como alternativas à rarefação, existem alguns índices que calculam a riqueza de espécies ponderando a abundância total (i.e. tamanho da amostra) dentro de cada comunidade.

Esses índices são:

1. Índice de Margalef

\[D_{Mg} = \frac{S-1}{ln (N)}\]

onde:

• S = o número de espécies na comunidade
• ln = logaritmo natural
• N = número total de indivíduos na comunidade
• D_Mg não tem um valor máximo e sua interpretação é comparativa, com valores maiores indicando maior riqueza de espécies

2. Índice de Menhinick

• \[D_{Mn} = \frac{S}{\sqrt{N}}\]

onde:

• S = o número de espécies na comunidade
• N = número total de indivíduos na comunidade
• D_Mn não tem um valor máximo e sua interpretação é comparativa, com valores maiores indicando maior riqueza de espécies

Exemplo prático 1

Explicação dos dados

Neste exemplo, avaliaremos a riqueza de espécies de 10 comunidades. Os dados de ocorrência das espécies nas comunidades foram simulados para demonstrar as propriedades das métricas de diversidade taxonômicas. Utilizaremos este conjunto de dados para todos os exemplos deste capítulo.

Pergunta

• A variação espacial na riqueza de espécies nas comunidades está associada com a variação na precipitação?

Predições

• Os valores de riqueza de espécies serão maiores nas comunidades localizadas em regiões que recebem grande volume de precipitação do que em regiões mais secas

Variáveis

• Data frame com as comunidades (unidade amostral) nas linhas e as espécies (variável resposta) nas colunas
• Data frame com as comunidades (unidade amostral) nas linhas e precipitação anual (variável preditora) na coluna

Checklist

• Verificar se os data frames de composição de espécies e variáveis ambientais estão com as unidades amostrais nas linhas e variáveis preditores nas colunas

• Verificar se as comunidades nos data frames de composição de espécies e variáveis ambientais estão distribuídos na mesma sequência/ordem nos dois arquivos

Análise

Abaixo, demonstramos os códigos no R para determinar a riqueza de espécies para cada comunidade a partir dos dados de composição de espécies. Os dados estão disponíveis no pacote ecodados.

## Ver os dados das comunidades
head(composicao_especies)
#>       sp1 sp2 sp3 sp4 sp5 sp6 sp7 sp8 sp9 sp10
#> Com_1  10  10  10  10  10  10  10  10  10   10
#> Com_2  91   1   1   1   1   1   1   1   1    1
#> Com_3   1   3   6  25   1   0   0   0   0    0
#> Com_4   0   0   0   0   0  15  15  18  17   16
#> Com_5   0   9   0   6   0  11   0   2  12    0
#> Com_6   3   0   5   0  12   1   0  13  12    0

Vamos ver a riqueza de espécies para cada comunidade.

## Calculando a riqueza observada de espécies para cada comunidade
riqueza_sp <- specnumber(composicao_especies)
riqueza_sp
#>  Com_1  Com_2  Com_3  Com_4  Com_5  Com_6  Com_7  Com_8  Com_9 Com_10 
#>     10     10      5      5      5      6      2      4      6      4

Vamos ver a abundância total de cada comunidade.

## Calculamos a abundância total para cada comunidade
abundancia <- apply(composicao_especies, 1, sum)
abundancia
#>  Com_1  Com_2  Com_3  Com_4  Com_5  Com_6  Com_7  Com_8  Com_9 Com_10 
#>    100    100     36     81     40     46      4     20     15     11

Calculando o Índice de Margalef.

## Índice de Margalef
# A função round é para limitar o resultado para duas casas decimais.
Margalef <- round((riqueza_sp - 1)/log(abundancia), 2)
Margalef
#>  Com_1  Com_2  Com_3  Com_4  Com_5  Com_6  Com_7  Com_8  Com_9 Com_10 
#>   1.95   1.95   1.12   0.91   1.08   1.31   0.72   1.00   1.85   1.25

Calculando o Índice de Menhinick.

## Índice de Menhinick
Menhinick <- round(riqueza_sp/sqrt(abundancia), 2)
Menhinick
#>  Com_1  Com_2  Com_3  Com_4  Com_5  Com_6  Com_7  Com_8  Com_9 Com_10 
#>   1.00   1.00   0.83   0.56   0.79   0.88   1.00   0.89   1.55   1.21

Agora vamos analisar a relação entre a riqueza de espécies e a precipitação anual.

## Juntando todos os dados em um único data frame
dados <- data.frame(precipitacao$prec, riqueza_sp, Margalef, Menhinick)

## Renomenado as colunas
colnames(dados) <- c("Precipitacao", "Riqueza", "Margalef", "Menhinick")

## ANOVA
anova_riq <- lm(Riqueza ~ Precipitacao, data = dados)
anova(anova_riq)
#> Analysis of Variance Table
#> 
#> Response: Riqueza
#>              Df Sum Sq Mean Sq F value  Pr(>F)  
#> Precipitacao  1 30.622 30.6224  8.9156 0.01744 *
#> Residuals     8 27.478  3.4347                  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Há uma relação positiva entre a riqueza de espécies e a precipitação anual (F_1,8 = 8,91, P = 0,01).

Analisar a relação entre o Índice de Margalef e a precipitação anual.

## ANOVA
anova_marg <- lm(Margalef ~ Precipitacao, data = dados)
anova(anova_marg)
#> Analysis of Variance Table
#> 
#> Response: Margalef
#>              Df  Sum Sq Mean Sq F value Pr(>F)
#> Precipitacao  1 0.37865 0.37865  2.1201 0.1835
#> Residuals     8 1.42879 0.17860

Não há uma relação positiva entre o índice de Margalef e a precipitação anual (F_1,8 = 2,12, P = 0,18).

Agora vamos analisar a relação entre o índice de Menhinick e a precipitação anual.

## ANOVA
anova_menh <- lm(Menhinick ~ Precipitacao, data = dados)
anova(anova_menh)
#> Analysis of Variance Table
#> 
#> Response: Menhinick
#>              Df  Sum Sq  Mean Sq F value Pr(>F)
#> Precipitacao  1 0.07626 0.076262  1.0992 0.3251
#> Residuals     8 0.55503 0.069378

Não há uma relação positiva entre o índice de Menhinick e a precipitação anual (F_1,8 = 1,09, P = 0,32).

Com base nos resultados, vamos plotar apenas o gráfico com os resultados da riqueza de espécies ao longo do gradiente de precipitação anual (Figura 12.1).

## Gráfico
ggplot(data = dados, aes(x= Precipitacao, y= Riqueza)) + 
    labs(x = "Precipitação anual (mm)", y = "Riqueza de espécies") +
    geom_point(size = 4, shape = 21, fill = "darkorange", alpha = 0.7) +
    geom_smooth(method = lm, se = FALSE, color = "black") +
    tema_livro()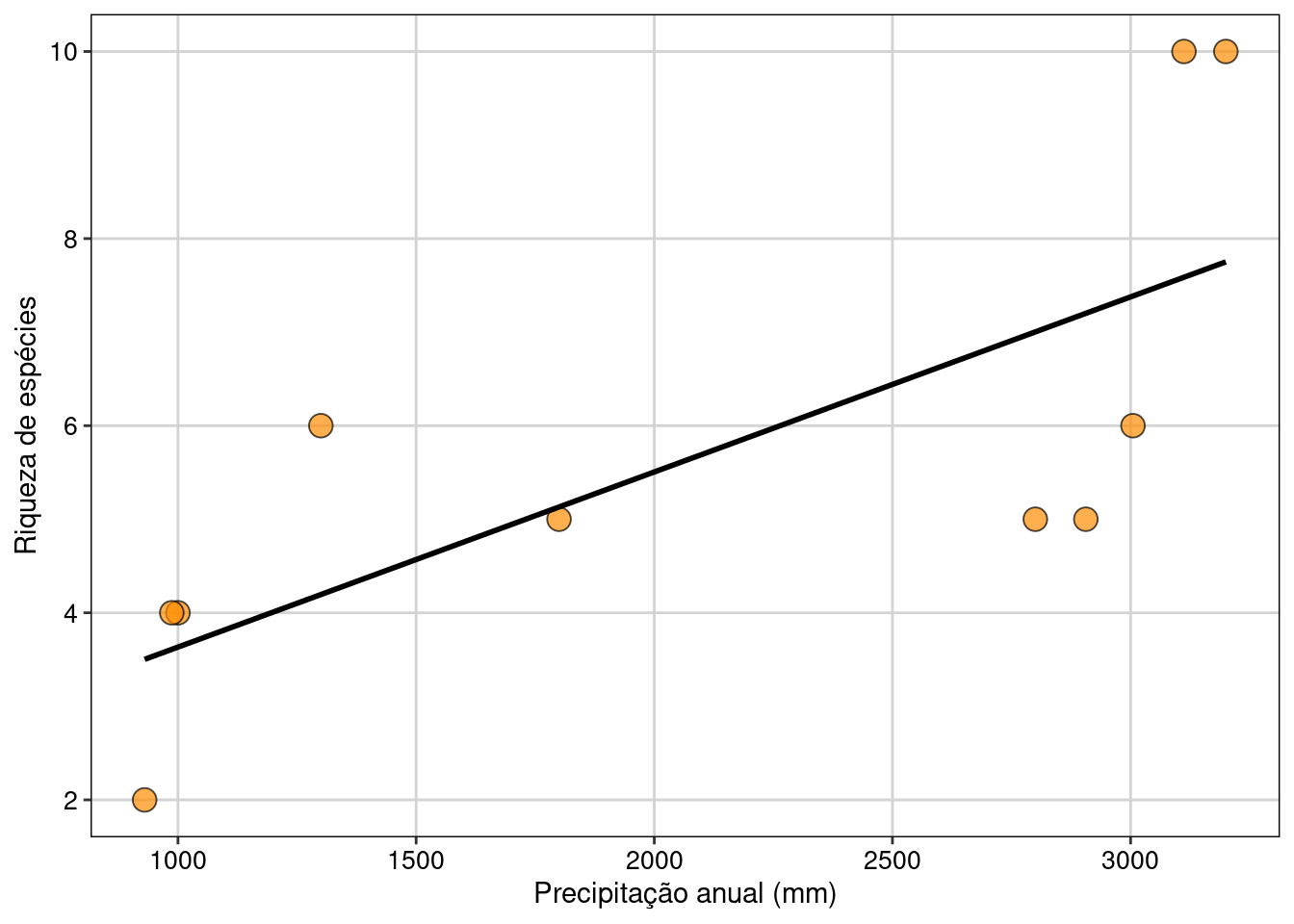

Figura 12.1: Gráfico do modelo linear da relação entre riqueza e precipitação.

Interpretação dos resultados

O número de espécies é maior em comunidades com maior precipitação. Contudo, quando ponderamos pela abundância (índices de Margalef ou Menhinick), a relação com a precipitação não é significativa.

📝 Importante
Percebam que ponderar a riqueza de espécies pela abundância altera a interpretação dos resultados.

12.2.2 Diversidade de espécies

Diferente dos índices de riqueza de espécies que não levam em consideração a abundância relativa das espécies (i.e. todas as espécies tem o mesmo peso), os índices de diversidade avaliam além da riqueza, a dominância ou raridade das espécies nas comunidades. Assim, quando comparamos duas comunidades com a mesma riqueza de espécies, e uma das comunidades é dominada por uma única espécie e a outra comunidade apresenta espécies com abundâncias parecidas, consideramos a segunda comunidade mais diversa. Os índices de diversidade variam porque eles dão pesos diferentes para a riqueza e equitabilidade das espécies. Assim, um determinado índice de diversidade pode indicar que uma comunidade X é mais diversa que uma comunidade Y, enquanto outro índice indica o oposto (Melo 2008). Portanto, uma maneira de determinar qual índice de diversidade usar é saber se você quer dar maior peso para riqueza ou equitabilidade das espécies nas comunidades.

📝 Importante
Ressaltamos que há várias críticas em relação ao uso dos índices de diversidade que são abstratos e difíceis de se interpretar (Hurlbert 1971). Por exemplo, dizer que o valor X estimado por índices de diversidade é alto ou baixo é irrelevante se não tivermos uma base comparativa (para mais detalhes veja Melo (2008)).

Os dois índices de diversidade mais usados em Ecologia são:

1. Índice de Shannon-Wiener

Quantifica a incerteza associada em predizer a identidade de uma espécie dado o número de espécies e a distribuição de abundância para cada espécie. Este índice é mais sensível às mudanças nas espécies raras da comunidade.

\[H' = -\sum_{i=1}^{S}p_i * ln p_i\]

onde:

• p_i = abundância relativa de cada espécie, calculada pela proporção dos indivíduos de uma espécie pelo número total dos indivíduos na comunidade
• ln = logaritmo natural, mas outras bases logarítmicas podem ser utilizadas
• H’ = não tem um valor máximo e sua interpretação é comparativa, com valores maiores indicando maior diversidade

2. Índice de Simpson

Quantifica a probabilidade de dois indivíduos retirados ao acaso da comunidade pertencerem à mesma espécie. Este índice é na verdade uma medida de dominância. Assim como a probabilidade dos indivíduos serem da mesma espécie diminui com o aumento da riqueza de espécies, o índice de Simpson também diminui com a riqueza.

\[D = \sum_{i=1}^{S}p_i^2\]

onde:

• P_i = abundância relativa de cada espécie, calculada pela proporção dos indivíduos de uma espécie pelo número total dos indivíduos na comunidade

• D = varia de 0 a 1, com valores próximos de 1 indicando menor diversidade enquanto valores próximos de 0 indicam maior diversidade. Para evitar confusão nas interpretações, normalmente o índice de Simpson é expressado como o valor inverso (1 - D) para que os maiores valores representem maior diversidade. Neste caso, o valor inverso é conhecido na literatura como índice Gini-Simpson. Para o índice Gini-Simpson estamos avaliando a probabilidade de dois indivíduos retirados ao acaso da comunidade sejam de espécies diferentes.

Exemplo prático 2

Explicação dos dados

Usaremos os mesmos dados simulados do exemplo prático 1.

Pergunta

• A variação espacial na diversidade de espécies das comunidades está associada com o gradiente de precipitação?

Predições

• Os valores de diversidade de espécies serão maiores nas comunidades localizadas em regiões maior volume de precipitação do que em regiões mais secas

Análise

Abaixo demonstramos os códigos no R para determinar a diversidade de espécies para cada comunidade a partir da planilha de composição de espécies.

## Índice de Shannon
# MARGIN = 1 significa que a função irá calcular o índice considerando 
# as linhas do data.frame (comunidades).
shannon_res <- diversity(composicao_especies, index = "shannon", MARGIN = 1)
shannon_res
#>     Com_1     Com_2     Com_3     Com_4     Com_5     Com_6     Com_7     Com_8     Com_9    Com_10 
#> 2.3025851 0.5002880 0.9580109 1.6068659 1.4861894 1.5607038 0.6931472 1.1058899 1.7140875 1.2636544

O argumento index = "simpson", calcula o índice Gini-Simpson (1-D).

## Índice de Simpson
simpson_res <- diversity(composicao_especies, index = "simpson", MARGIN = 1) 
simpson_res
#>     Com_1     Com_2     Com_3     Com_4     Com_5     Com_6     Com_7     Com_8     Com_9    Com_10 
#> 0.9000000 0.1710000 0.4814815 0.7989636 0.7587500 0.7674858 0.5000000 0.5850000 0.8088889 0.6942149

Interpretação dos resultados

A comunidade 1 foi a comunidade que apresentou a maior diversidade de espécies (Shannon-Wiener = 2,3 e Gini-Simpson = 0.9), enquanto a comunidade 2 foi a comunidade que apresentou a menor diversidade (Shannon-Wiener = 0,5 e Gini-Simpson = 0,17). Gostaríamos de chamar a atenção para a importância da distribuição da abundância relativa das espécies dentro das comunidades. Percebam que tanto a comunidade 1 quanto a comunidade 2 abrigam o mesmo número de espécies (10 espécies) e abundância total (100 indivíduos), mas os padrões de distribuição da abundância relativa entre as espécies dentro das comunidades são bem discrepantes. Na comunidade 1 as espécies apresentam abundâncias semelhantes entre elas (i.e. alta equitabilidade), enquanto na comunidade 2 uma espécie é dominante e as outras raras (i.e. baixa equitabilidade). Essa diferença na distribuição da abundância relativa entre as comunidades é um fator muito importante para os índices de diversidade.

Dentro desta perspectiva, alguns índices fornecem uma estimativa sobre a equitabilidade da distribuição da abundância nas comunidades. Entre eles, o mais conhecido foi proposto por Pielou (1966).

Índice de Equabilidade (ou Equitabilidade) de Pielou

É uma métrica derivada do índice de Shannon-Wiener que descreve o padrão de distribuição da abundância relativa das espécies na comunidade.

\[J = \frac{H'}{Hmax} = \frac{H'}{ln (S)}\]

onde:

• H’ = índice de Shannon-Wiener
• H_max = todas as espécies teriam a mesma abundância relativa
• H_max é calculado aplicando o logaritmo natural (ln) para a riqueza de espécies (S)
• Se todas as espécies apresentam a mesma abundância relativa, então J = 1. Se uma espécie apresenta forte dominância, J aproxima-se de zero

Não há uma função no R que calcule o índice de Pielou, mas ele pode facilmente ser calculado usando os valores de diversidade de Shannon-Wiener e o logaritmo da riqueza de espécies de cada comunidade.

## Índice de Pielou
Pielou <- shannon_res/log(specnumber(composicao_especies))

Agora que temos uma ideia de como a riqueza de espécies e a distribuição da abundância relativa são importantes para quantificar os valores dos índices de diversidade, vamos testar se há alguma relação entre os índices de diversidade e precipitação anual nas comunidades.

## Juntando todos os dados em um único data frame
dados_div <- data.frame(precipitacao$prec, shannon_res, 
                        simpson_res, Pielou)

## Renomeando as colunas
colnames(dados_div) <- c("Precipitacao", "Shannon", "Simpson", "Pielou")

Vamos realizar uma regressão simples para verificar a relação entre o índice de Shannon-Wiener e a precipitação anual nas comunidades.

## ANOVA
anova_shan <- lm(Shannon ~ Precipitacao, data = dados_div)
anova(anova_shan)
#> Analysis of Variance Table
#> 
#> Response: Shannon
#>              Df  Sum Sq Mean Sq F value Pr(>F)
#> Precipitacao  1 0.10989 0.10989  0.3627 0.5637
#> Residuals     8 2.42366 0.30296

Agora, vamos realizar uma regressão simples para verificar a relação entre o índice de Simpson e a precipitação anual nas comunidades.

## ANOVA
anova_simp <- lm(Simpson ~ Precipitacao, data = dados_div)
anova(anova_simp)
#> Analysis of Variance Table
#> 
#> Response: Simpson
#>              Df  Sum Sq  Mean Sq F value Pr(>F)
#> Precipitacao  1 0.00132 0.001325  0.0252 0.8778
#> Residuals     8 0.42064 0.052580

Por fim, vamos fazer regressão simples para verificar a relação entre o índice de Pielou e a precipitação anual nas comunidades.

## ANOVA
anova_piel <- lm(Pielou ~ Precipitacao, data = dados_div)
anova(anova_piel)
#> Analysis of Variance Table
#> 
#> Response: Pielou
#>              Df  Sum Sq  Mean Sq F value Pr(>F)
#> Precipitacao  1 0.09080 0.090798  1.5792 0.2443
#> Residuals     8 0.45997 0.057496

📝 Importante
As análises acima são apenas ilustrativas. Não estamos avaliando as premissas de normalidade e homogeneidade da variância dos resíduos (veja Capítulo 7). Além disso, é importante estar ciente das críticas e limitações de usar índices de Shannon e Simpson como nesses exemplos (Lou Jost 2007).

Interpretação dos resultados

A variação espacial na diversidade de espécies, obtida através dos índices de Shannon-Wiener e Simpson, e a equitabilidade de Pielou não foram associados com a variação na precipitação anual entre as áreas (P > 0,05).

12.2.3 Diagramas de Whittaker ou Curva de Dominância

Embora os índices de diversidade de espécies englobem os componentes de riqueza e abundância relativa das espécies nas suas estimativas, não é possível conhecer o número de espécies ou quais são as espécies dominantes ou raras dentro das comunidades. Por exemplo, duas comunidades podem ter o mesmo valor de diversidade e ainda assim apresentarem diferenças na riqueza e equitabilidade (Melo 2008). O Diagrama de Whittaker é um método que lida com essas questões utilizando informações visuais do número de espécies e abundância relativa de cada espécie nas comunidades. Este método plota as espécies ranqueadas no eixo X da mais abundante para a menos abundante, enquanto no eixo Y as abundâncias relativas das espécies são plotadas em escala logarítmica (log₁₀). Este gráfico permite ao leitor reconhecer: i) a riqueza de espécies observando o eixo X, ii) a equitabilidade da abundância relativa das espécies pela inclinação da reta, e iii) quais são as espécies dominantes, intermediárias e raras nas comunidades através da observação em relação ao eixo Y. A partir destas curvas, vários autores propuseram modelos matemáticos para explicar a distribuição de abundância das espécies gerando diferentes modelos teóricos (e.g. série geométrica, broken-stick, log-series e log-normal). Cada modelo possui predições distintas: o modelo geométrico prediz distribuição de abundâncias desiguais, broken-stick prediz distribuição de abundâncias uniformes, enquanto log-normal e log-series são intermediárias com predições distintas sobre as proporções de espécies raras - alta em log-series, baixa em log-normal (veja McGill et al. (2007) para revisão).

Para análises exploratórias onde você tem interesse em visualizar o padrão da distribuição relativa das espécies por comunidade, a função rankabundance do pacote BiodiversityR é uma opção interessante (Figura 12.2).

## Cálculo da curva para as comunidades 2 e 3
rank_com2 <- rankabundance(composicao_especies[2, composicao_especies[2,] > 0])
rank_com3 <- rankabundance(composicao_especies[3, composicao_especies[3,] > 0])

## Gráfico 
# Veja a ajuda da função rankabundplot para outros exemplos de gráficos.
rankabunplot(rank_com2, scale = "logabun", specnames = c(1), 
             pch = 19, col = "darkorange")
rankabunplot(rank_com3, scale = "logabun", specnames = c(1), pch = 19, 
             xlim = c(0,10), addit = TRUE, col = "cyan4" , legend = TRUE)
legend(5, 40, legend = c("Comunidade 2", "Comunidade 3"),
       col = c("darkorange", "cyan4"), lty = 1, cex = 0.8, box.lty = 0)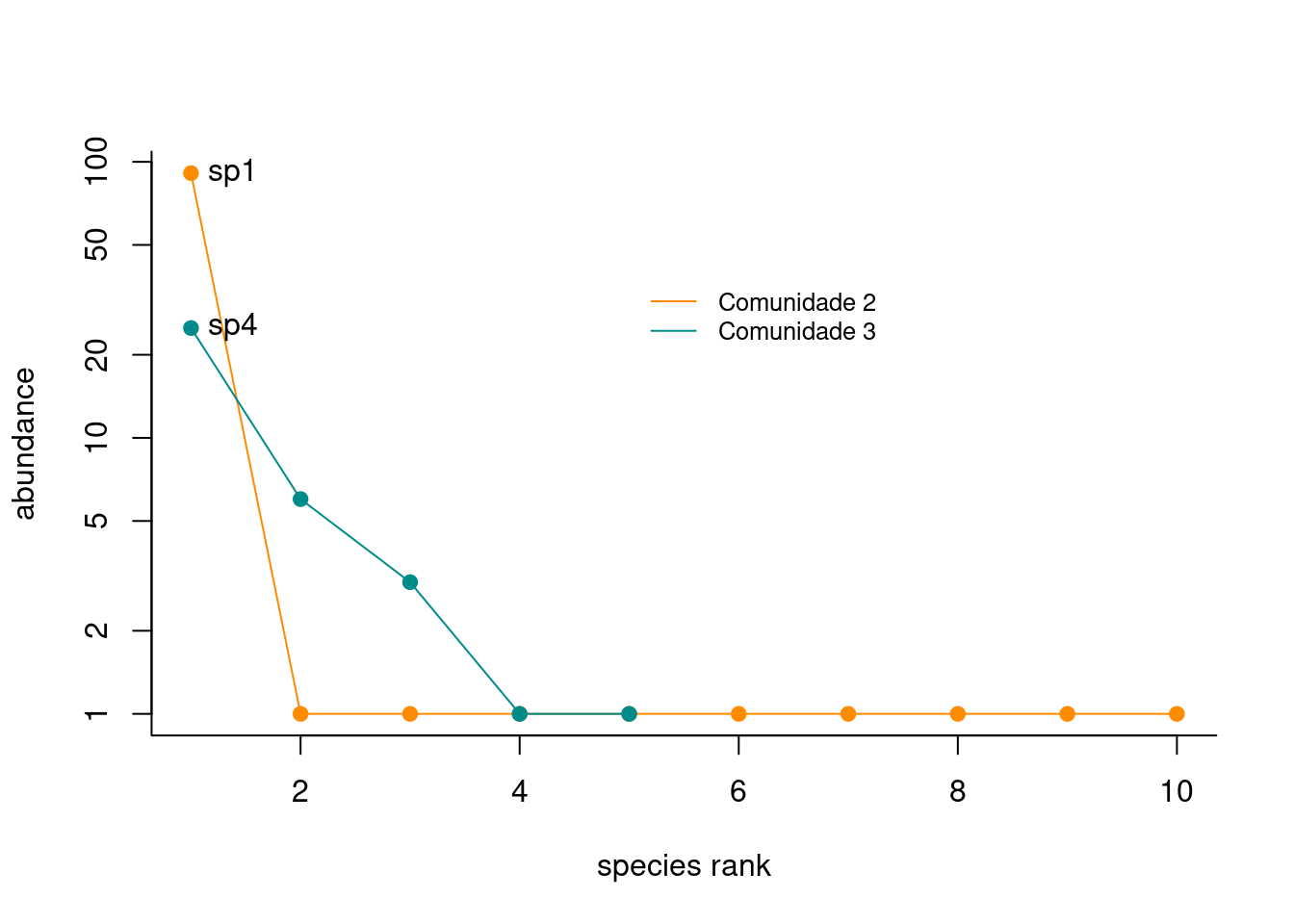

Figura 12.2: Diagramas de Whittaker para duas comunidades.

Interpretação dos resultados

Percebam que olhando os eixos do gráfico conseguimos determinar que a Comunidade 2 (círculo laranja) abriga 10 espécies no total (i.e. comprimento do eixo X), com a espécie sp1 apresentando alta dominância e as outras espécies apresentando abundâncias muito baixas. A Comunidade 3 (círculo ciano) abriga cinco espécies no total, sendo que a espécie sp4 apresenta alta dominância, duas espécies apresentam abundâncias intermediárias e outras duas abundâncias baixas.

12.2.4 Curvas de distribuição de abundâncias

Caso o interesse seja avaliar qual dos modelos teóricos melhor explica a distribuição das abundâncias das espécies, a função radift() do pacote vegan é a melhor opção.

A função radfit avalia cinco modelos teóricos para determinar qual deles melhor se ajustam aos dados. Os modelos teóricos avaliados na função são:

• Null = modelo broken-stick
• preemption = série geométrica
• log-normal
• Zipf
• Zipf-Mandelbrot

Você pode realizar as análises separadamente para cada comunidade ou para todas as comunidades ao mesmo tempo.

Vamos começar avaliando separadamente a Comunidade 2.

## Teste das curvas de distribuição de abundâncias
curvas_dominancia_com2 <- radfit(composicao_especies[2,])
curvas_dominancia_com2
#> 
#> RAD models, family poisson 
#> No. of species 10, total abundance 100
#> 
#>            par1     par2    par3        Deviance AIC     BIC    
#> Null                                    175.242  199.592 199.592
#> Preemption  0.68962                      79.560  105.910 106.213
#> Lognormal  -0.65366  3.2485              47.350   75.701  76.306
#> Zipf        0.83829 -3.0254              26.612   54.963  55.568
#> Mandelbrot  0.83829 -3.0254  1.6442e-07  26.612   56.963  57.871

Agora vamos fazer um gráfico com as predições dos modelos (Figura 12.3).

plot(curvas_dominancia_com2, 
     ylab = "Abundância", 
     xlab = "Ranqueamento das espécies")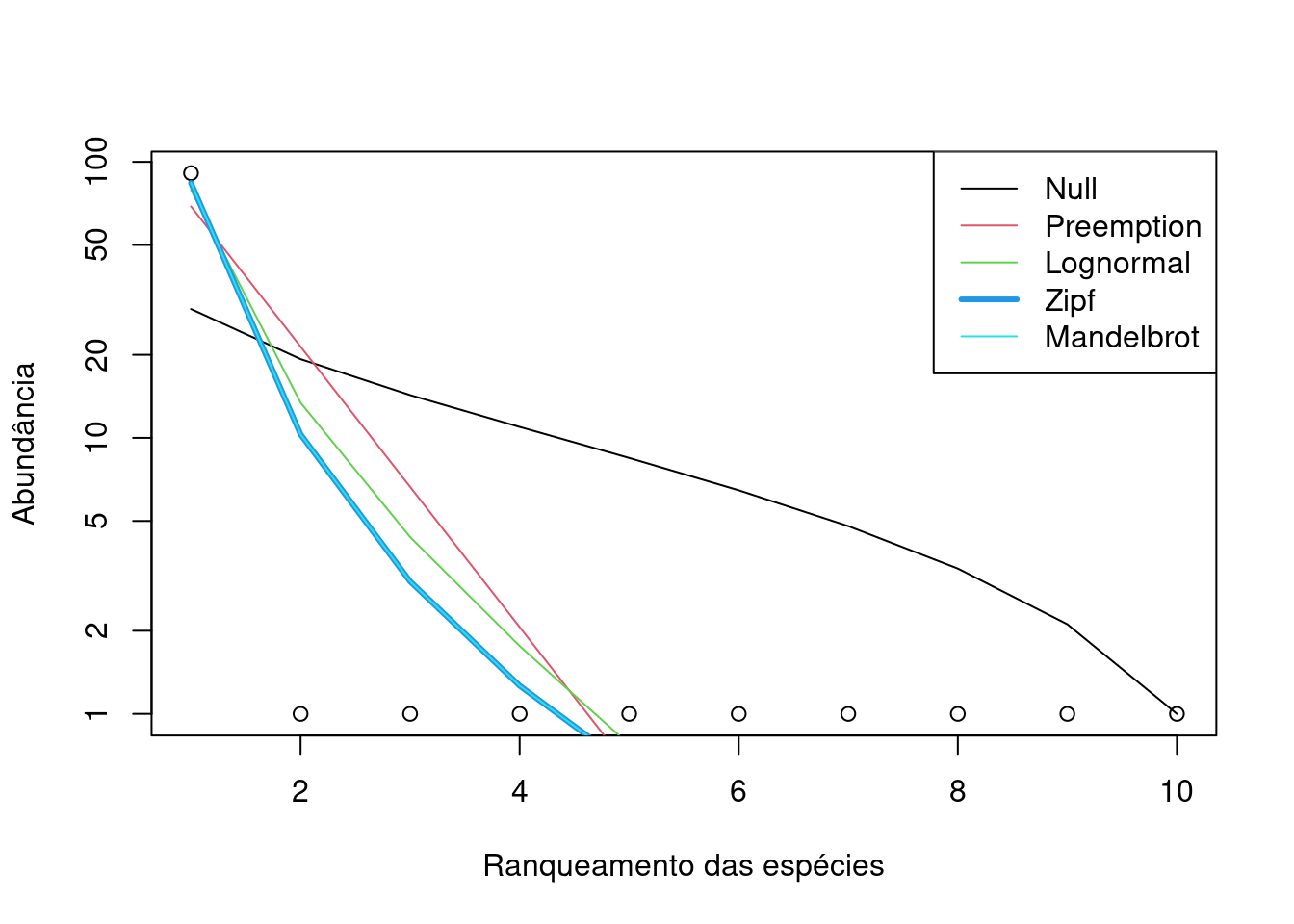

Figura 12.3: Teste de cinco Diagramas de Whittaker para a Comunidade 2.

Interpretação dos resultados

Os pontos brancos representam as espécies ranqueadas de acordo com a abundância e as linhas representam as predições dos modelos matemáticos. Com base nos valores de AIC (veja Capítulo 7), o modelo Zipf é o melhor modelo que explica a distribuição da abundância relativa das espécies na Comunidade 2.

Agora vamos analisar os dados considerando todas as comunidades (Figura 12.4).

## Teste das curvas de distribuição de abundâncias
curvas_dominancia_todas <- radfit(composicao_especies)
curvas_dominancia_todas
#> 
#> Deviance for RAD models:
#> 
#>                  Com_1       Com_2       Com_3       Com_4       Com_5       Com_6       Com_7       Com_8       Com_9 Com_10
#> Null        8.2193e+01  1.7524e+02  8.9085e+00  4.2265e+01  4.9719e+00  4.7099e+00  1.1507e+00  1.8998e+00  2.7703e+00 1.1146
#> Preemption  2.2878e+01  7.9560e+01  1.5423e+00  1.4332e+01  3.0438e+00  4.5536e+00  7.7259e-01  1.7847e+00  9.2518e-01 0.7428
#> Lognormal  -1.7764e-15  4.7350e+01  1.0161e+00  2.9441e-02  1.9303e+00  4.8898e+00 -2.2053e-25  1.4556e+00  2.0626e-01 0.5079
#> Zipf        8.8818e-15  2.6612e+01  2.1659e-01  1.5846e-02  3.6094e+00  8.3245e+00 -2.2073e-25  6.6938e-01  4.7931e-01 0.8730
#> Mandelbrot -1.7764e-15  2.6612e+01  2.0926e-01  1.1390e-02  1.8740e+00  4.1131e+00  0.0000e+00  6.6938e-01  2.3634e-01 0.4456

# Vamos fazer um gráfico para cada comunidade
plot(curvas_dominancia_todas, log = "y")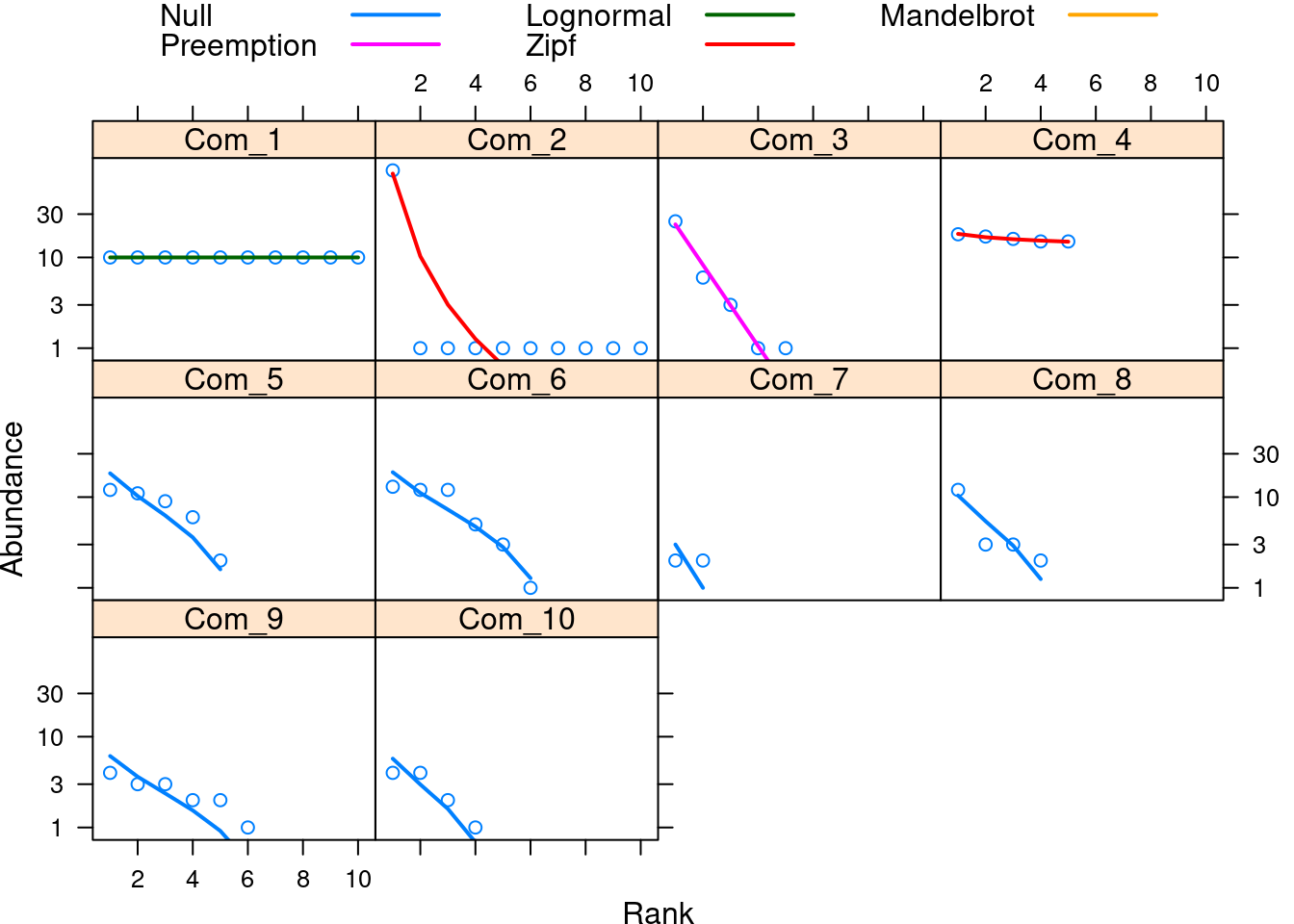

Figura 12.4: Testes de cinco Diagramas de Whittaker para todas as comunidades.

Interpretação dos resultados

A Comunidade 1 foi associada com o modelo log-normal, as Comunidades 2 e 4 com o modelo Zipf, a Comunidade 3 com o modelo série geométrica e as outras comunidades com o modelo nulo. Para explorar a explicação biológica por trás destes modelos veja os artigos (Wilson 1991; McGill et al. 2007; Magurran and McGill 2011).

📝 Importante
A ligação entre o modelo matemático e a explicação biológica precisa ser interpretada com cuidado porque diferentes modelos matemáticos podem levar ao mesmo padrão de distribuição de abundância.

12.2.5 Números de Hill ou Série de Hill

Embora os índices de Shannon-Wiener e Gini-Simpson sejam amplamente usados em estudos ecológicos e de conservação, eles sofrem de propriedades matemáticas e não representam a diversidade propriamente dita (L. Jost 2006). Portanto, quando o objetivo é avaliar a diversidade, os índices de Shannon-Wiener e Gini-Simpson não deveriam ser utilizados na sua forma padrão, mas transformados em números efetivos de espécies ou diversidade verdadeira (L. Jost 2006). O número efetivo de espécies é o número de espécies igualmente abundantes (i.e. todas as espécies com a mesma abundância) necessárias para produzir o valor observado para um determinado índice. Por exemplo, uma comunidade com índice de Shannon-Wiener estimado de 4,5 teria um número efetivo de 90 espécies igualmente abundantes. Jost et al. (2006) usam o seguinte exemplo para explicar o conceito do número efetivo de espécies - uma comunidade com 16 espécies igualmente abundantes é duas vezes mais diversa do que uma comunidade com 8 espécies igualmente abundantes. Neste caso, a diversidade deveria ser proporcional ao número de espécies. Contudo, quando aplicamos os índices de diversidade para estas comunidades com 16 e 8 espécies (cada espécie com 5 indivíduos), o índice de Shannon-Wiener é 2,772 e 2,079, respectivamente, e o índice de Gini-Simpson é 0,937 e 0,875, respectivamente. Claramente, os valores estimados pelos índices de diversidade não representam a diferença entre as comunidades porque eles carecem de uma particularidade matemática conhecida como propriedade de duplicação.

O próximo exemplo (modificado do website de Lou Jost; http://www.loujost.com/), demostra a importância da transformação dos índices de diversidade em números efetivos de espécies. Imagine que você foi contratado para avaliar a diversidade de peixes em um riacho antes e depois da instalação de uma usina hidrelétrica. Suponha que os valores estimados pelo índice de Gini-Simpson foi de 0,99 antes da instalação e de 0,97 depois da instalação. A princípio, você poderia concluir que a diversidade diminuiu somente 2% e que a instalação da hidrelétrica não afetou a diversidade de peixes no riacho. Contudo, transformando os valores do índice de diversidade em números efetivos, percebemos que antes da instalação a diversidade do riacho equivale a 100 espécies igualmente abundantes, enquanto após a instalação, a diversidade equivale a 33 espécies igualmente abundantes. Portanto, a queda da diversidade foi de 66% e não 2%.

Hill (1973) derivou uma equação geral para o cálculo do número efetivo de espécies ou diversidade verdadeira que depende apenas do valor de q e da abundância relativa das espécies.

\[^qD = (\sum_{i=1}^{S}p_i^q)^{1/(1-q)}\]

Onde:

• q = é um parâmetro conhecido como ordem da diversidade e é usado para dar peso às espécies comuns ou raras. q = 0 não considera a frequência das espécies e representa a riqueza observada de espécies, q = 1 equivale a transformação do índice de Shannon-Wiener (i.e. exp(H')) e atribui pesos às espécies com base na proporção das suas frequências e, q = 2 equivale à transformação do índice de Gini-Simpson (i.e. 1/(1-D)) e atribui peso às espécies mais comuns. Valores de q \<1 favorecem espécies raras, enquanto valores de q \> 1 favorecem espécies comuns.

• p_i = abundância relativa de cada espécie, calculada pela proporção dos indivíduos de uma espécie pelo número total dos indivíduos na comunidade

Vamos calcular o Número de Hill para as comunidades do nosso exemplo.

Calculando o Número de Hill com q = 0.

## Número de Hill para q = 0
hill_res_q_0 <- hill_taxa(composicao_especies, q  = 0)
hill_res_q_0
#>  Com_1  Com_2  Com_3  Com_4  Com_5  Com_6  Com_7  Com_8  Com_9 Com_10 
#>     10     10      5      5      5      6      2      4      6      4

Calculando o Número de Hill com q = 1.

## Número de Hill para q = 1
hill_res_q_1 <- hill_taxa(composicao_especies, q  = 1)
hill_res_q_1
#>     Com_1     Com_2     Com_3     Com_4     Com_5     Com_6     Com_7     Com_8     Com_9    Com_10 
#> 10.000000  1.649196  2.606507  4.987156  4.420220  4.762172  2.000000  3.021912  5.551608  3.538328

Calculando o Número de Hill com q = 2.

## Número de Hill para q = 2
hill_res_q_2 <- hill_taxa(composicao_especies, q  = 2)
hill_res_q_2
#>     Com_1     Com_2     Com_3     Com_4     Com_5     Com_6     Com_7     Com_8     Com_9    Com_10 
#> 10.000000  1.206273  1.928571  4.974223  4.145078  4.300813  2.000000  2.409639  5.232558  3.270270

Criando um data frame com os três resultados anteriores.

## Resultados
res_hill <- data.frame(hill_res_q_0, hill_res_q_1, hill_res_q_2)
colnames(res_hill) <- c("q=0", "q=1", "q=2")
head(res_hill)
#>       q=0       q=1       q=2
#> Com_1  10 10.000000 10.000000
#> Com_2  10  1.649196  1.206273
#> Com_3   5  2.606507  1.928571
#> Com_4   5  4.987156  4.974223
#> Com_5   5  4.420220  4.145078
#> Com_6   6  4.762172  4.300813

Interpretação dos resultados

Como na comunidade 1 todas as espécies são igualmente abundantes, alterar os valores de q não altera o número efetivo de espécies que permanece sempre 10. Contudo, na comunidade 2, que apresenta alta dominância de uma espécie, alterar os valores de q diminui consideravelmente a estimativa da diversidade. A vantagem dos Números de Hill é que eles são de fácil interpretação e comparação entre as comunidades. Fator ausente para os índices de diversidade.

📝 Importante
Neste ponto, esperamos que tenha ficado claro que mais do que a riqueza de espécies, a abundância relativa das espécies (e.g. comuns ou raras) tem um papel fundamental na estimativa da diversidade de espécies.

12.3 Diversidade beta

O termo diversidade beta foi proposto por Whittker (1960) e foi definido como a razão entre a diversidade gama e a diversidade alfa (i.e. diversidade beta multiplicativa), quantificando não só a relação entre a diversidade regional e local, mas também o grau de diferenciação entre as comunidades. Para demonstrar como a diversidade beta varia entre comunidades locais dentro de uma região usaremos a explicação do Baselga (http://webspersoais.usc.es/persoais/andres.baselga/beta.html). Imagine três comunidades, cada comunidade abrigando as mesmas cinco espécies. Neste caso, a média da diversidade alfa = 5, a diversidade gama = 5 e a razão entre elas (gama/alfa) indica uma diversidade beta = 1. Isso significa que na região existe apenas uma unidade distinta de composição. Quando a composição de espécies das três comunidades é completamente diferente (i.e. diferenciação máxima), temos que a média da diversidade alfa = 5, a diversidade gama = 15 e a razão entre elas indica uma diversidade beta = 3. Neste caso, existem três unidades distintas dentro da região. Assim, a diversidade beta multiplicativa varia de 1 até o número de comunidades dentro da região.

A maioria dos índices de (dis)similaridade utilizadas na ecologia (e.g. índices de Jaccard e Sørensen) são índices que padronizam a diversidade beta e geram valores independentes do número de comunidades. Eles podem ser calculados para dados de incidência (presença e ausência) ou abundância (Legendre and Legendre 2012) e considerando comparações par-a-par entre as comunidades ou comparação entre múltiplas comunidades (i.e. multiple-site). Por muito tempo, os valores de (dis)similaridade foram interpretados como sinônimo de substituição de espécies (turnover) entre comunidades. Contudo, índices de (dis)similaridade como Jaccard e Sørensen geram valores de (dis)similaridade para comunidades que não apresentam diferenças na composição de espécies, mas apresentam diferenças na riqueza de espécies (i.e. comunidades aninhadas). Pensando nestes fatores, Baselga (2010, 2012) propôs uma abordagem que particiona a diversidade beta total (\(\beta\)_jac) em dois componentes: o componente resultante da substituição de espécies (turnover - \(\beta\)_tur) e o componente resultante do aninhamento (nestedness, i.e. diferença na riqueza de espécies - \(\beta\)_nes). Vejam a (Figura 12.5) onde temos 3 comunidades (X, Y e Z). No primeiro exemplo, temos apenas diferença no número de espécies entre as comunidades. Neste caso, o componente subsituição de espécies (\(\beta\)_tur) é zero porque as espécies na comunidade Z são um sub-grupo das espécies nas comunidades X e Y. O mesmo para as espécies na comunidade Y que são um sub-grupo das espécies da comunidade X. No segundo exemplo, temos o cenário oposto com as comunidades abrigando a mesma riqueza de espécies e assim, o componente resultante do aninhamento (\(\beta\)_nes) é zero, temos um valor máximo para o \(\beta\)_tur. Percebam que somando \(\beta\)_tur com \(\beta\)_nes temos o valor da diversidade beta total (\(\beta\)_jac). Baselga (2013) também propôs a partição da diversidade beta para índices de dissimilaridade que lidam com dados de abundância. Neste caso os componentes da diversidade beta são chamados de variação balanceada na abundância (similar ao componente substituição de espécies) e gradiente de abundância (similar ao componente aninhamento). Reconhecer estes componentes da diversidade beta é importante porque eles apresentam padrões distintos (substituição de espécies versus perda ordenada de espécies), que provavelmente estão sendo gerados por processos ecológicos diferentes (Baselga 2010, 2012, 2013).

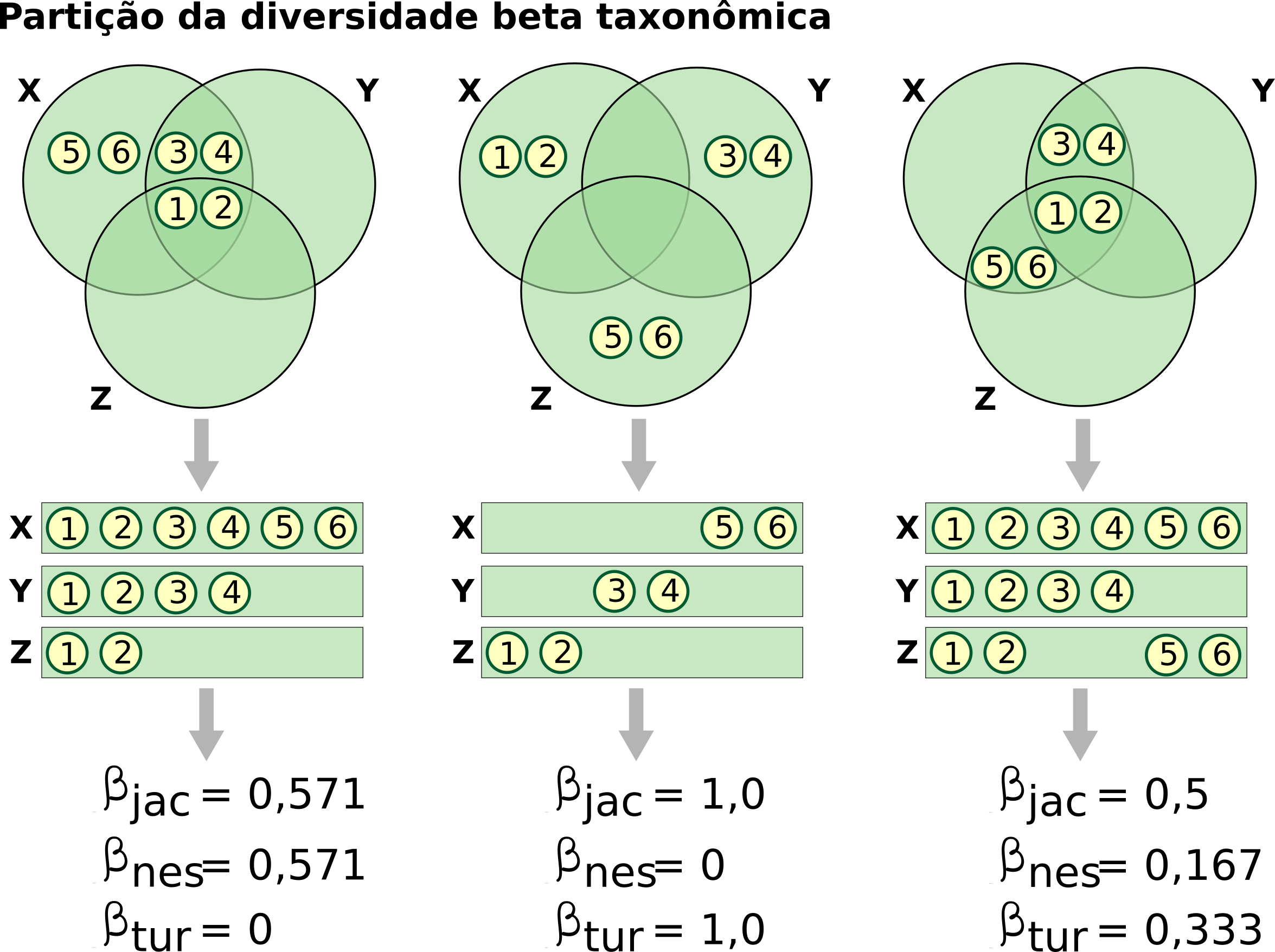
Figura 12.5: Partição da diversidade beta taxonômica. Os três cenários apresentados representam a diversidade beta explicada somente por substituição, aninhamento e uma combinação dos dois.

Aqui, vamos demonstrar alguns exemplos de como calcular a partição da diversidade beta para os dados deste capítulo.

Para isso, primeiro vamos transformar nossos dados de abundância em presença e ausência.

## Transformando dados em presencia e ausência.
composicao_PA <- decostand(composicao_especies, method = "pa")

Calculando a diversidade beta par a par usando os dados de presença e ausência.

## Diversidade beta
resultado_PA <- beta.pair(composicao_PA, index.family = "sorensen")

📝 Importante
A função beta.pair() gera três listas com matrizes triangulares:

• Diversidade beta total = índice de Sørensen (beta.sor)
• Componente de substituição = índice de Simpson (beta.sim)
• Componente de aninhamento = diferença na riqueza (beta.sne)

Vamos olhar os resultados da diversidade beta total.

## Resultados
resultado_PA$beta.sor
#>            Com_1     Com_2     Com_3     Com_4     Com_5     Com_6     Com_7     Com_8     Com_9
#> Com_2  0.0000000                                                                                
#> Com_3  0.3333333 0.3333333                                                                      
#> Com_4  0.3333333 0.3333333 1.0000000                                                            
#> Com_5  0.3333333 0.3333333 0.6000000 0.4000000                                                  
#> Com_6  0.2500000 0.2500000 0.4545455 0.4545455 0.4545455                                        
#> Com_7  0.6666667 0.6666667 0.7142857 0.7142857 1.0000000 0.7500000                              
#> Com_8  0.4285714 0.4285714 0.7777778 0.3333333 0.3333333 0.2000000 1.0000000                    
#> Com_9  0.2500000 0.2500000 0.4545455 0.4545455 0.2727273 0.5000000 0.7500000 0.4000000          
#> Com_10 0.4285714 0.4285714 0.3333333 0.7777778 0.5555556 0.4000000 0.6666667 0.7500000 0.6000000

Vamos montar um data frame com os resultados

## Data frame com os resultados
data.frame_PA <- data.frame(round(as.numeric(resultado_PA$beta.sor), 2),
                            round(as.numeric(resultado_PA$beta.sim), 2),
                            round(as.numeric(resultado_PA$beta.sne), 2))
colnames(data.frame_PA) <- c("Sorensen", "Simpson", "Aninhamento")
head(data.frame_PA)
#>   Sorensen Simpson Aninhamento
#> 1     0.00       0        0.00
#> 2     0.33       0        0.33
#> 3     0.33       0        0.33
#> 4     0.33       0        0.33
#> 5     0.25       0        0.25
#> 6     0.67       0        0.67

📝 Importante
Percebam que a primeira linha e primeira coluna do data frame (i.e., 0.00) representa a dissimilaridade de Sørensen entre a Com1 e Com2 (compare com os valores da matriz triangular acima). As linhas subsequentes representam a dissimilaridade da Com1 com todas as outras comunidades, depois da Com2 com todas as comunidades e assim sucessivamente. Lembrem-se que os componentes, subsituição (Simpson) e aninhamento, são um desdobramento da diversidade beta total (Sørensen). Assim, a soma da dissimilaridade de Simpson e aninhamento é igual ao valor de dissimilaridade de Sørensen (Baselga 2010, 2012).

Vamos calcular a dissimilaridade entre a precipitação anual das comunidades usando o índice de distância euclidiana. Vejam a ajuda da função vegdist() que calcula 17 índices diferentes de dissimilaridade.

## Dissimilaridade
prec_dis <- vegdist(precipitacao, method = "euclidian")
dados_prec <- as.numeric(prec_dis) 

Agora vamos juntar os resultados.

📝 Importante
As comunidades devem estar dispostas na mesma ordem nas duas planilhas (composição de espécies e precipitação) para que os resultados representem as dissimilaridades par a par para as mesmas comunidades no data frame.

Criando data frame.

## Data frame
dados_dis <- data.frame(dados_prec, data.frame_PA)
head(dados_dis)
#>   dados_prec Sorensen Simpson Aninhamento
#> 1         88     0.00       0        0.00
#> 2        400     0.33       0        0.33
#> 3       1400     0.33       0        0.33
#> 4        294     0.33       0        0.33
#> 5        195     0.25       0        0.25
#> 6       2270     0.67       0        0.67

Vamos testar a relação entre as diferenças na composição de espécies e precipitação nas comunidades.

## ANOVA
# Avaliar a relação entre os valores de diversidade beta total (Sørensen) e precipitação.
anova_sore <-lm(Sorensen ~ dados_prec, data = dados_dis)
anova(anova_sore)
#> Analysis of Variance Table
#> 
#> Response: Sorensen
#>            Df  Sum Sq  Mean Sq F value Pr(>F)
#> dados_prec  1 0.00188 0.001877  0.0358 0.8508
#> Residuals  43 2.25264 0.052387

# Avaliar a relação entre os valores do componente substituição (Simpson) e precipitação
anova_simp <-lm(Simpson ~ dados_prec, data = dados_dis)
anova(anova_simp)
#> Analysis of Variance Table
#> 
#> Response: Simpson
#>            Df Sum Sq  Mean Sq F value Pr(>F)
#> dados_prec  1 0.1403 0.140342  1.4905 0.2288
#> Residuals  43 4.0488 0.094157

# Avaliar a relação entre os valores do componente aninhamento e precipitação
anova_anin <-lm(Aninhamento ~ dados_prec, data = dados_dis)
anova(anova_anin)
#> Analysis of Variance Table
#> 
#> Response: Aninhamento
#>            Df  Sum Sq Mean Sq F value  Pr(>F)  
#> dados_prec  1 0.17467 0.17467  6.4006 0.01515 *
#> Residuals  43 1.17349 0.02729                  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Interpretação dos resultados

Há uma relação positiva entre o componente aninhado da diversidade beta e a diferença na precipitação entre as comunidades (F_1,43 = 6,4, P = 0,01). Contudo, não há relação entre a diversidade beta total (Sørensen) e o componente substituição de espécies (Simpson) com a precipitação (P > 0,05).

Agora vamos fazer um gráfico com o componente aninhamento da diversidade beta (Figura 12.6).

## Gráfico
ggplot(data = dados_dis, aes(x = dados_prec, y = Aninhamento)) + 
    geom_point(size = 4, shape = 21, fill = "darkorange") +
    geom_smooth(method = lm, se = FALSE, color = "black") +
    labs(x = "Diferença precipitação (mm)", 
         y = "Componente aninhamento da\n diversidade beta") +
    tema_livro()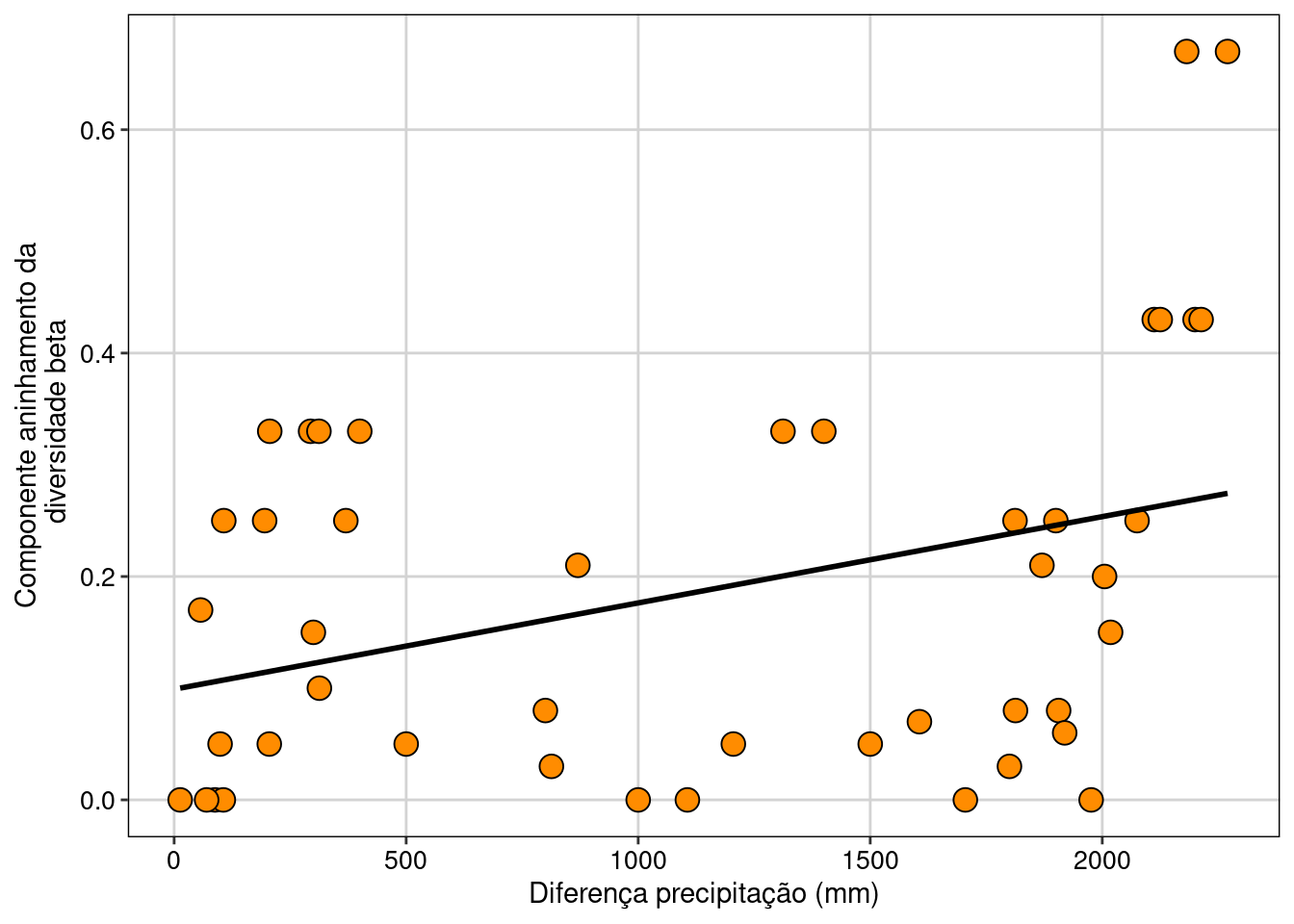

Figura 12.6: Relação entre o componente de aninhamento da diversidade beta e a diferença da precipitação.

Interpretação dos resultados

As comunidades localizadas em locais com baixa precipitação anual apresentam espécies que são um subgrupo das espécies presentes nas comunidades com alta precipitação anual.

Agora vamos fazer um exemplo considerando os dados de abundância das espécies.

A função beta.pair.abund() gera três listas com matrizes triangulares:

• Diversidade beta total = índice de Bray-Curtis (beta.bray)
• Componente variação balanceada (beta.bray.bal)
• Componente gradiente de abundância (beta.bray.gra)

Análise.

## Diversidade beta para abundância
resultado_AB <- beta.pair.abund(composicao_especies, index.family = "bray")

Cria um data frame com os resultados.

## Data frame
# Vamos montar um data.frame com os resultados.
data.frame_AB <- data.frame(round(as.numeric(resultado_AB$beta.bray), 2),
                            round(as.numeric(resultado_AB$beta.bray.bal), 2),
                            round(as.numeric(resultado_AB$beta.bray.gra), 2))
colnames(data.frame_AB) <- c("Bray", "Balanceada", "Gradiente")
head(data.frame_AB)
#>   Bray Balanceada Gradiente
#> 1 0.81       0.81      0.00
#> 2 0.69       0.42      0.27
#> 3 0.45       0.38      0.06
#> 4 0.47       0.07      0.40
#> 5 0.47       0.15      0.31
#> 6 0.92       0.00      0.92

## Agora vamos juntar os resultados com a precipitação
dados_dis_AB <- data.frame(dados_prec, data.frame_AB)

Testar a relação da dissimilaridade considerando a abundância com a diferença na precipitação entre as comunidades.

## ANOVA
# Avaliar a relação entre os valores de diversidade beta total e precipitação
anova_dis_AB <- lm(Bray ~ dados_prec, data = dados_dis_AB)
anova(anova_dis_AB)
#> Analysis of Variance Table
#> 
#> Response: Bray
#>            Df  Sum Sq  Mean Sq F value Pr(>F)
#> dados_prec  1 0.01782 0.017815  0.8441 0.3634
#> Residuals  43 0.90755 0.021106

# Avaliar a relação entre os valores do componente balanceada e precipitação
anova_balan <- lm(Balanceada ~ dados_prec, data = dados_dis_AB)
anova(anova_balan)
#> Analysis of Variance Table
#> 
#> Response: Balanceada
#>            Df  Sum Sq Mean Sq F value  Pr(>F)  
#> dados_prec  1 0.48761 0.48761  7.0742 0.01094 *
#> Residuals  43 2.96391 0.06893                  
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# Avaliar a relação entre os valores do componente gradiente e precipitação
anova_grad <- lm(Gradiente ~ dados_prec, data = dados_dis_AB)
anova(anova_grad)
#> Analysis of Variance Table
#> 
#> Response: Gradiente
#>            Df  Sum Sq Mean Sq F value    Pr(>F)    
#> dados_prec  1 0.68981 0.68981  18.705 8.903e-05 ***
#> Residuals  43 1.58575 0.03688                      
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Interpretação dos resultados

Há uma relação positiva entre os componentes variação balanceada (F_1,43 = 7,07, P = 0,01) e gradiente (F_1,43 = 18,7, P < 0,001) de abundância da diversidade beta com a diferença na precipitação entre as comunidades. Contudo, não há relação entre a diversidade beta total (Bray) com a precipitação (F_1,43 = 0,84, P = 0,36).

Vamos fazer um gráfico para a variação balanceada da diversidade beta (Figura 12.7).

ggplot(data = dados_dis_AB, aes(x = dados_prec, y = Balanceada)) + 
    geom_point(size = 4, shape = 21, fill = "darkorange") +
    geom_smooth(method = lm, se = FALSE, color = "black") +
    labs(x = "Diferença precipitação (mm)",
         y = "Componente variação balanceada\n da diversidade beta") +
    tema_livro()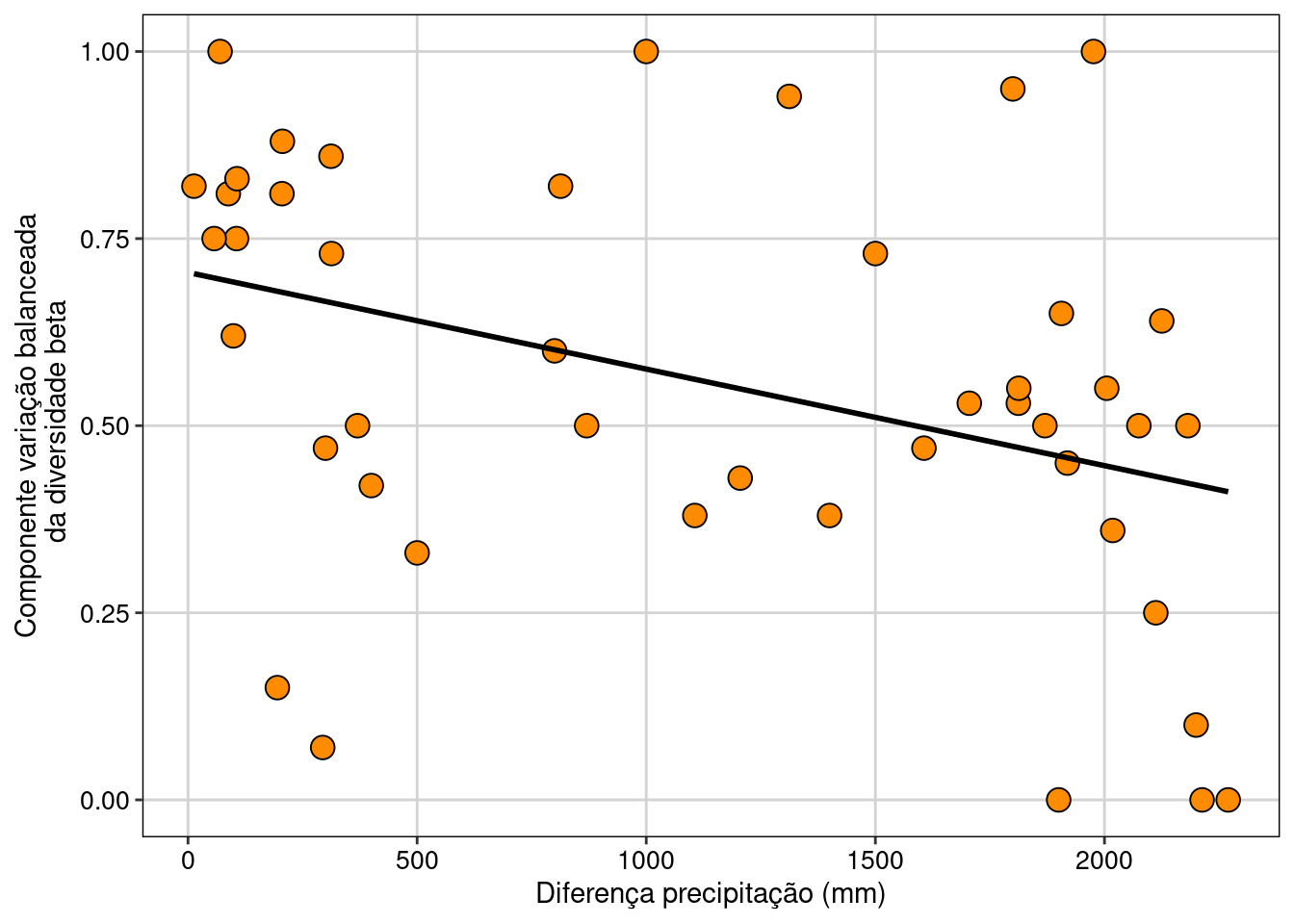 

Figura 12.7: Relação entre o componente variação balanceada da diversidade beta e a diferença da precipitação.

Interpretação dos resultados

Olhando o início do eixo X onde as comunidades apresentam precipitação anual similares (i.e. baixa diferença na precipitação), o componente variação balanceada indica que há uma tendência das espécies com maiores abundâncias não serem as mesmas quando comparamos duas comunidades (i.e. maiores valores de dissimilaridade). Por outro lado, quando a diferença na precipitação entre duas comunidades é alta, o componente variação balanceada é baixo, indicando que as mesmas espécies estão dominando a abundância nas comunidades comparadas.

Vamos fazer agora um gráfico para a variação gradiente da diversidade beta (Figura 12.8).

ggplot(data = dados_dis_AB, aes(x = dados_prec, y = Gradiente)) + 
    geom_point(size = 4, shape = 21, fill = "darkorange") +
    geom_smooth(method = lm, se = FALSE, color = "black") +
    labs(x = "Diferença precipitação anual (mm)", 
         y = "Componente gradiente de abundância\n da diversidade beta") +
    tema_livro()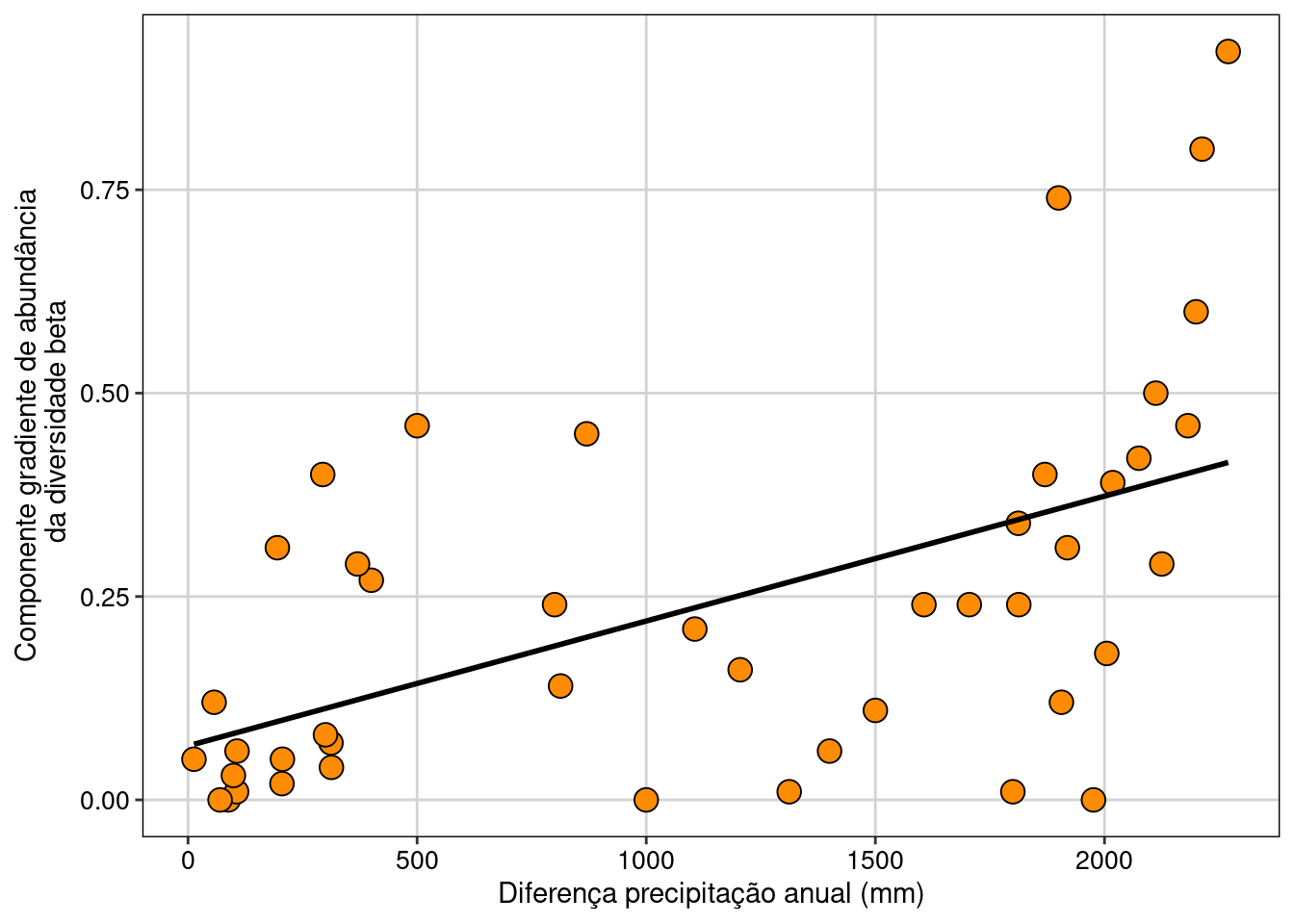

Figura 12.8: Relação entre o componente variação gradiente da diversidade beta e a diferença da precipitação.

Interpretação dos resultados

Olhando o início do eixo X onde as comunidades apresentam precipitação anual similares (i.e. baixa diferença na precipitação), o componente gradiente indica que há uma tendência das espécies apresentarem abundâncias parecidas (i.e. menor valor de dissimilaridade). Por outro lado, quando a diferença na precipitação entre duas comunidades é alta, o componente gradiente é alto, indicando que as mesmas espécies têm valores discrepantes de abundâncias entre as comunidades.

12.4 Para se aprofundar

12.4.1 Livros

• Recomendamos a leitura dos artigos citados no capítulo e os livros de Magurran & McGill (2011) - Biological Diversity Frontiers in Measurement and Assessment e Legendre & Legendre (2012) - Numerical Ecology.

12.4.2 Links

Recomendamos a página pessoal do pesquisador Lou Jost que apresenta e discute diversas medidas de diversidade taxonômica:

• Medidas de diversidade e similaridade
• Medindo a diversidade de uma única localidade
• Comparando a diversidade entre duas comunidades
• Número efetivo de espécies

12.5 Exercícios

12.1 Carregue os dados - anuros_composicao - que está no pacote ecodados. Este conjunto de dados representa a abundância de 211 espécies de anuros coletados em 44 localidades na Mata Atlântica. Calcule a riqueza de espécies para cada comunidade e os índices de Margalef, Menhinich, Shannon-Wiener, Gini-Simpson e Equitabilidade de Pielou. Salve todos os resultados em novo data frame. Faça um gráfico usando o função ggpairs para ver a correlação entre as métricas. Qual a sua interpretação sobre os resultados?

12.2 Usando os resultados anteriores, selecione as duas comunidades com os maiores e menores valores de Shannon-Wiener. Em seguida, faça um Diagrama de Whittaker. Por fim, interprete as curvas considerando as curvas teóricas (i.e., geométrica, broken-stick, etc.) descritas nos livros de ecologia.

12.3 Usando os dados - anuros_composicao - calcule a partição da diversidade beta considerando os dados de abundância e presença e ausência. a) Faça um gráfico boxplot com os resultados. Discuta se os resultados usando abundância ou presença e ausência são congruentes ou discrepantes. b) Calcule a distância geográfica (use a planilha anuros_ambientais) entre as localidades (use a Distância Euclidiana). Em seguida, faça uma análise de regressão para verificar se as localidades que estão próximas apresentam maior similaridade na composição de espécies (use componente turnover - Bsim) do que as comunidades que estão distantes (e.g., Decaimento da similaridade).

Soluções dos exercícios.